How to draw the side angle side triangles? Properties of side angle side triangle construction, The side-angle-side (SAS) theorem.

Side Angle Side (SAS) Triangle Congruence
For two triangles to be congruent SAS the angle must be included between the two sides. If the angle is not between the two sides then a specific triangle cannot be drawn unless one of the angles is a right angle.
Example: Construct ABC triangle in which a = 5 cm, mB = 50° and c = 4 cm.
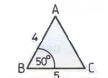
- (a) Draw the sketch and mark the given elements.
- b) Draw a line at least 5 cm long and mark point B near one end.
- (c) With centre B and radius 5 cm mark off point C on the line.
- (d) Using a protractor measure angle B and draw the ray from B at 50° with [BC.
- (e) With centre B and radius 4 cm mark point A along this ray.
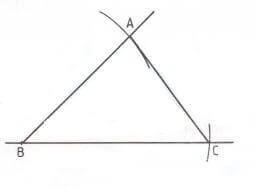
- (f) Join A to C.
The side-angle-side (SAS) theorem
The side-angle-side (SAS) theorem states that if two sides of a triangle have lengths a and b, and the angle between these sides has measure C, then the triangle is uniquely determined, up to congruence. This means that if you know the lengths of two sides of a triangle and the angle between those sides, you can use the SAS theorem to determine the triangle.
There are a few conditions that need to be satisfied for the SAS theorem to be applicable:
- The two sides must be opposite the angle.
- The angle must be included between the two sides.
- The sum of the two sides must be greater than the third side.
If these conditions are satisfied, then you can use the theorem to find the third side of the triangle. The formula for finding the third side is:
c = √(a^2 + b^2 – 2abcos(C))
where c is the length of the third side, a and b are the lengths of the other two sides, and C is the measure of the angle between the two sides.