Learn about how the eye works, including the role of the retina and the functions of different parts of the eye. Discover the science behind vision and how the brain interprets the information sent from the eyes.
HOW THE EYE FUNCTIONS
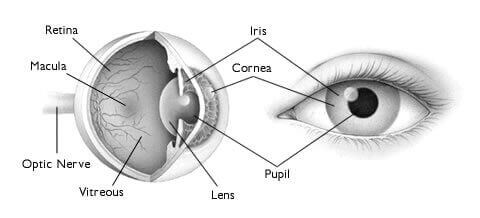
Vision is a highly complex process in which light rays entering the eye are focused on the retina where they are converted into nerve impulses that are then coded and carried to the brain.
Focusing the Image.
Light reaching the cornea is bent at the cornea surface due to the large difference in the indexes of refraction between the two media—the air and the cornea—and to the angle at which it reaches the cornea. Most of the focusing of the image is accomplished here since there are relatively few differences in the refractive indexes of the cornea, the lens, and the aqueous and vitreous humors.
However, a fine focusing device under control by the nervous system is required to bring the image into precise register upon the retina. This device is the lens. When the ciliary muscles, which are attached to the lens by ligaments, contract, the tension on the lens is lessened and the lens becomes more spherical through its own elasticity. Relaxation of the ciliary muscles increases the tension on the lens and flattens it. The process whereby nerve impulses control ciliary muscle contraction and relaxation, and thus the degree of lens curvature, is called accommodation.
In some people the eyeball is too long for the lens to focus an image of a distant object precisely on the retina. Instead, the image falls in front of the retina. These people are said to be nearsighted because their vision of near objects is not affected. In people who are far-sighted, the eyeball is sometimes too short and the image of a near object is focused so that it would fall behind the retina. In older people farsightedness is usually due to a natural loss of elasticity of the lens. Nearsightedness and farsightedness can generally be corrected by means of eyeglasses or contact lenses.
Regulating the Amount of Light.
The amount of light entering the eye can be controlled somewhat by partially closing the eyelid and by varying the diameter of the pupil. The size of the pupil is regulated by the circular muscles of the iris, which contract by degrees to stop down, or close, the opening. The pupil diameter can vary 4-fold, which amounts to a 16-fold variation in its area.
The flow of nerve impulses that control both accommodation and pupil diameter is governed by sensory information relayed from the retina to the central nervous system where, in turn, it gives rise to motor impulses in the nerves that innervate the appropriate muscles. Involuntary reflex paths provide for continual adjustments of lens curvature, pupil diameter, and eye position.
Role of the Retina.
Light rays reaching the retina first pass through several layers before reaching the photoreceptors, which point away from the light. A reasonable explanation for this apparent inversion of the retina is that the photoreceptors must maintain contact with the densely pigmented epithelium for their growth and for the regeneration of their visual pigments. If the photoreceptors were to face the light, the opaque epithelium would lie between the light and the photoreceptors, resulting in a severe reduction in light intensity.
The outer portions of the photoreceptors are densely packed with photosensitive pigments that capture the light. These pigments are similar in chemistry but differ in the region of the visible spectrum to which they are most sensitive. In the human eye the rods all contain the same pigment, but cones may contain one of three pigments: one maximally sensitive to blue light, another to green light, and a third to yellow light. The cone pigments function in color vision.
When some light is captured by the pigment molecules inside a photoreceptor, chemical and structural changes in the molecules are initiated. These changes result in an alteration of the permeability of the cell’s membrane to certain ions in its environment. The result of this change of permeability is a transient voltage whose magnitude is proportional to the rate at which the photoreceptor absorbs light. This phenomenon is an example of what is referred to as the neural code—that is, the transformation of the qualities of an external stimulus, in this case light intensity, into nerve impulses intelligible to the brain.
At the junctions between the photoreceptor, horizontal cells, and bipolar cells are synaptic regions that, when activated by voltage changes, release transmitter chemicals that traverse the tiny synaptic gaps and excite the bipolar and horizontal cells. A voltage change is then initiated in these cells which, in turn, causes electrical discharges in a ganglion cell. The electrical impulses are then transmitted to the brain where they activate the appropriate brain regions. The trains of electrical impulses produced by the nerve cells that encode the visual stimulus are analogous to those impulses carried in a telephone cable that code a speaking voice.
Because the visual system functions over an enormous range of intensities—from dim moonlight to bright sunlight—the eye must adjust its operating range to suit the changing conditions. However, it cannot at the same time be fully responsive to extremes of intensity because the demands placed on the visual system by perception in bright and dim lights are mutually exclusive. Vision in dim light demands high sensitivity that is gained by gathering light energy over a large area of the retina for a relatively long period of time. For the perception of fine detail and rapid movement, on the other hand, the visual system must distinguish the nervous activity of small adjacent retinal areas and must respond rapidly. This can occur only when light intensity is high.
The eye resolves this dilemma by using two subsystems:
one that functions well at bright daylight intensity levels and a second that operates when light is dim. Daylight vision is accomplished principally by the foveal region, where there is a dense concentration of cones. Rods, which are numerous everywhere except in the fovea, function in weak light and are inactivated by bright light. When a person moves from bright sunlight into a darkened room or from a dark room into bright light, a few minutes are required for the eye to switch from one system to another.
The neural pathways of the two systems play a crucial role in organizing the visual image. Each retinal nerve cell receives many synaptic influences from its neighboring cells. Some of these are stimulating, others are inhibitory. The response of the nerve cell to these influences reflects a balance between the diverse inputs. Through the use of excitatory and inhibitory influences, the retina can emphasize certain aspects of the visual stimulus that are important to the observer, and it can deemphasize other aspects not so important.
Another critical way in which nerve networks organize the visual response is through the point-to-point representation of the retinal surface upon the visual cortex, the part of the brain’s cerebral cortex concerned with vision. During the embryonic development of the eye and brain, retinal nerve fibers growing toward the brain terminate according to a genetically determined pattern in which nerves from adjacent retinal areas occupy neighboring positions in a particular brain area. The functional significance of this arrangement is seen in animal studies where nervous interaction between neighboring retinal areas is found to be a fundamental mechanism in contour discrimination, color vision, and the detection of movement.
mavi