What is Einstein’s Theory Of Gravitation: Principle Of Equivalence? Information on gravitational waves.
Einstein’s Theory Of Gravitation:
Principle Of Equivalence; Einstein wondered why inertial mass should be proportional to gravitational mass. In 1911, after careful study, he found a reasonable assumption from which the proportionality would follow as a logical consequence. He suggested that an accelerated frame in a small region free of gravitational fields is equivalent to a rest frame in a gravitational field. This is the principle of equivalence. It implies that all experiments within the two frames will have identical results, provided the acceleration of the moving frame equals the acceleration of falling bodies in the rest frame.
Source : pixabay.com
Einstein used the principle of equivalence to investigate the path of light in a gravitational field. Imagine light entering an accelerating rocket ship in free space. A passenger measures its path as a curved line because between the time it enters one side of the ship and leaves on the other, the ship has moved forward and changed its velocity. But by the principle of equivalence, the same curved path must be measured by a physicist located in a gravitational field at rest. Therefore light falls in a gravitational field. More sophisticated arguments are needed to calculate light deflection over extended regions.
By 1916, Einstein had developed a complete mathematical theory of gravitation, the general theory of relativity, in which the effect of a mass is to deform the geometrical properties of the space surrounding it. Using the ideas of the non-Euclidian geometers, he suggested that the path of a light ray is a geodesic—that is, light always travels the shortest time path between two points. However, while that shortest path is usually a straight line in Euclidean flat space, it is curved in non-Euclidean curved space.
Einstein and the German astrophysicist Karl Schwarzchild were able to obtain a solution to Einstein’s equations for certain simple cases, such as the gravitational field of a spherically symmetric mass. Their solution indicated that Einstein’s theory differed from Newtonian theory in at least three measurable effects. The first, and still the clearest, vindication of Einstein’s theory was the anomalous advance of Mercury’s perihelion. His theory accounted for all of the 43 seconds of arc now unaccounted for by Newtonian theory. The second effect concerned the curvature of light in a gravitational field. Einstein predicted that starlight passing close to the sun would be bent, seeming to displace the star outward from its normal position by an angle about Viooo of the sun’s diameter. Stars near the sun can be seen easily during a total eclipse,, and the famous solar eclipse of 1922 provided data that supported Einstein’s theory.
Finally, Einstein’s theory predicts a “red shift” of light traveling upward in a gravitational field—that is, the wavelength of light is lengthened and shifted toward the red end of the visible spectrum. For two points on the earth’s surface differing in height by 100 feet this red shift amounts to about one part in 1014. This fantastically small frequency shift has been observed by several groups of physicists using the very sharp gamma rays of the Mossbauer effect.
Gravitational Waves.
Einstein’s theory predicted the existence of gravitational waves. Like electromagnetic waves, these waves propagate at the speed of light. They should be given off by double stars and by collapsing or exploding stars or galaxies. However, the expected intensity of such waves is so unimaginably small that physicists had virtually despaired of detecting them. In the 1960’s, though, some experiments were carried out that have raised exciting questions and refocused interest in gravitational waves.

Source : pixabay.com
A gravitational wave detector was invented by Dr. Joseph Weber at the University of Maryland in 1958. The detector consists of a suspended instrumented cylinder whose length is changed by a gravity wave (see figure). Weber’s instruments measure changes in length of Vioo of a trillionth of an inch routinely.
To guard against the possiblity that signals may be instrument noise or electromagnetic or seismic effects, more than one detector is employed, and they are separated by 600 miles. In a 3-month period, 17 simultaneous increases in intensity were observed at the separated detectors. The frequency of occurrence of the gravitational waves was totally unexpected by Weber and his coworkers, and this has raised grave problems for astrophysicists. Many suggestions for the sources of the waves have been advanced, including supernovas, pulsars, and collapsing binary neutron stars, but more observations are needed to identify the sources.
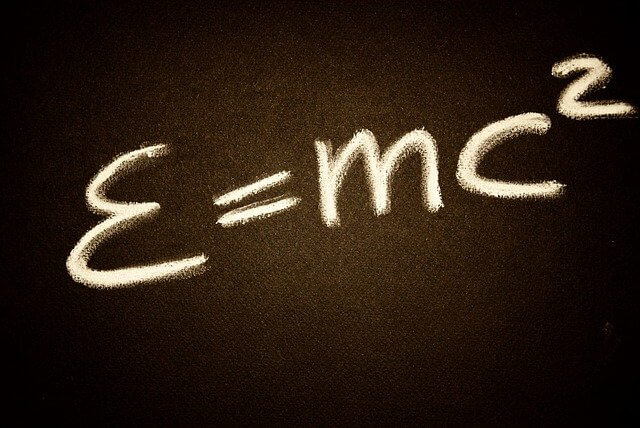
Source : pixabay.com
Scalar-Tensor Theory of Gravitation.
Einstein’s theory has been criticized by the physicists P. Jordan, R. H. Dicke, and Carl Brans. They propose a theory in which G can be calculated from the distribution of matter in the universe. G is also predicted to change with time. Thus, the gravitational force between, say, the sun and the earth may have been stronger several billion years ago, causing a corresponding change in the mean radius of the earth’s orbit.
Dicke called into question the main experimental verification of Einstein’s theory—the observed advance of Mercury’s perihelion. He asserted that this advance is affected by the non-spherical shape of the sun. In 1967, Dicke carried out an important experiment that indicates that the pole-to-pole diameter of the sun is a few parts in 100,000 smaller than the equatorial diameter. If this is interpreted as a gravitational effect then the advance of Mercury’s perihelion would be affected by it, according to Einstein’s theory. The close agreement between theory and observation would be destroyed, and the changed values would tend to support the theory of Jordan, Brans, and Dicke. However, the astrophysicists I. W. Roxburgh and Edward Spiegel have questioned the interpretation of the sun’s oblateness as a gravitational effect, and the matter remains unsettled.
Gravitation and Elementary Particles.
Modern quantum physics achieved phenomenal success in the understanding of thermal radiation, the spectral lines of atoms and molecules, and the chemical forces and the structure of matter. There has been less success in understanding the properties of the elementary particles. A large class of elementary particle calculations gives infinite results. Some success was achieved in using the special theory of relativity to separate the infinite, unobservable effects from the finite observable ones. Nonetheless, there is no complete mathematically consistent scheme for doing elementary particle calculations, and the theoretical difficulties appear to involve high-energy effects.

Source : pixabay.com
Ordinarily, gravitational effects are quite negligible in elementary particle interactions. Thus the electrostatic force between a pair of low-energy electrons is 10″ times the gravitational force. As the energy increases, however, the mass and gravitational interactions increase, while the charge remains the same. At an energy of 10″‘ electron volts the gravitational force is about equal to the electromagnetic force. Above this enormous energy, the gravitational interaction will dominate all others. For this reason, a program has been begitn to achieve a synthesis of quantum theory and general relativity. If successful, the program may remove the infinite results that plagued the quantum theory of fields, perhaps by the following considerations.
The curvature of space associated with gravitation limits the energy density that can be accumulated in a given region. Gravitation is an attractive force which tends to balance out the mutual repulsion of different parts of a charged particle. Thus it takes positive energy to bring elements of charge together to form a particle, but when gravitation is considered, its negative contribution and nonlinearity make even the energy of a point particle finite. In this way, or in others unforeseen, the quantization of Einstein’s general theory of relativity may yield new knowledge of space and time in the realm of very small dimensions and very high energies.