The nature of electromagnetic radiation, sources of radiation, properties of electromagnetic waves, interactions of radiation and matter, radiation and quantum theory. History of the study of electromagnetic radiation.
ELECTROMAGNETIC RADIATION is the transmission of energy in the form of paired electric and magnetic fîelds. The most familiar forms of electromagnetic radiation are light waves; heat, or infrared, radiation; and radio waves. However, the radiation also travels in shorter waves in the forms of ultraviolet light, X rays, and gamma rays. All of these forms of radiation have similar characteristics, ineluding the velocity at which they travel.
Radiation in general is one of the three ways in which energy can be transmitted, the other two being convection, or transmission through the motion of physical particles, and conduction, or transmission through the transfer of mechanical energy from partide to partide. Electromagnetic radiation, on the other hand, does not depend on a material medium for transmission. Instead it takes place as a wave motion through space, although in some circumstances the radiation behaves as though it were composed of particles rather than waves.
THE NATURE OF ELECTROMAGNETIC RADIATION
In order to understand electromagnetic radiation, it is necessary to know some of the important pıoperties of harmonic waves in general. A harmonic wave is a disturbance that is propagated through space, which may or may not be occupied by matter. At every point in the space through which the wave is passing, the disturbance has a toandfro motion, like uıat of a simple pendulum. The number of toandfro motions, or oscillations, per second is called the freçuency of the wave, and the time the wave takes to complete one oscillation is called its period. The distance traveled during one such period is called the wavelength. If the velocity at which the wave disturbance moves through space is denoted by v, it follows that the frequency f and the wavelength X are related by the simple but important formula
(1)
—a relation that holds for harmonic waves of all kinds. The unit of frequency is the Hertz (Hz), one Hz being one complete oscillation per second. For electromagnetic radiation, the unit of wavelength ranges from kilometers or miles to millionths of a centimeter or of an inch—or even less.
The Electromagnetic Field.
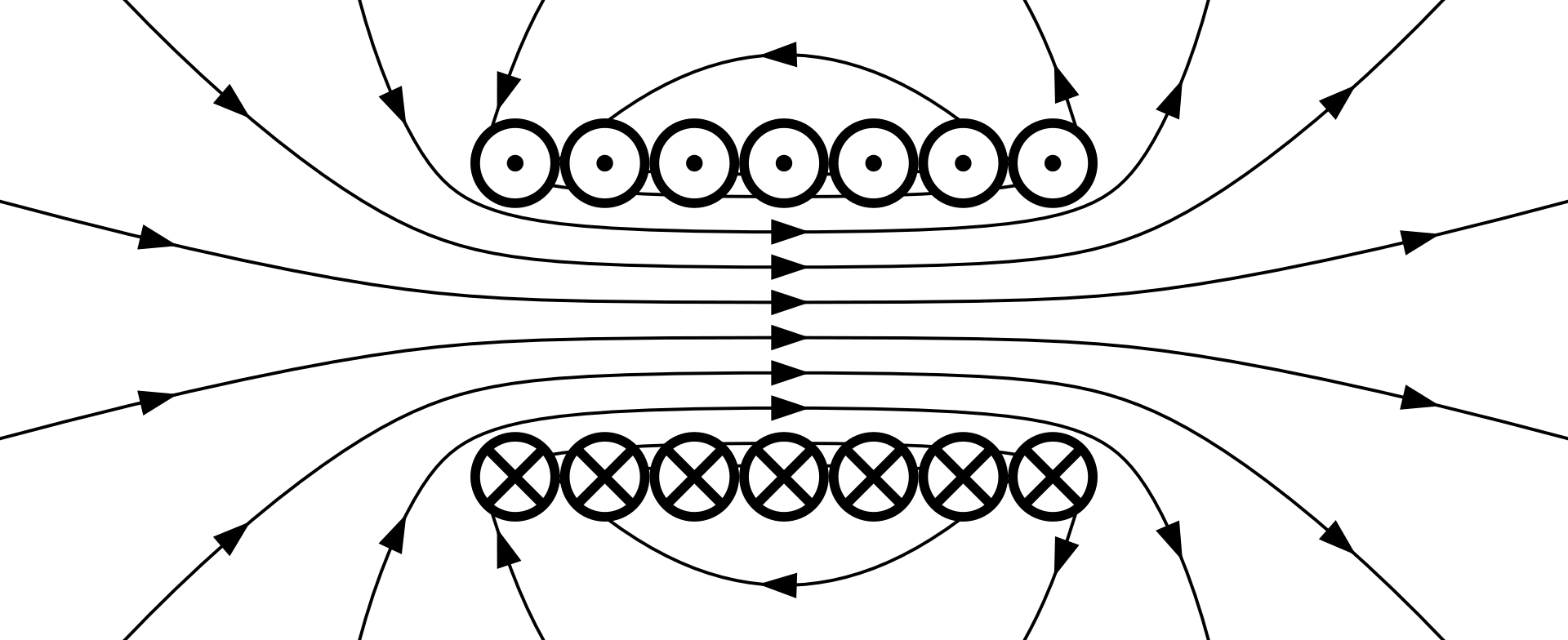
The disturbance propagated by an electromagnetic wave takes place in an electromagnetic field. The region surrounding an electric charge—for example, an electron—that is at rest is said to constitute an electric field, in the sense that at every point in this region another electric charge would experience a force of attraction to or repulsion from the charge producing the field. If the charge producing the field is in motion rather than at rest, the space around it will also constitute a magnetic field, in the sense that a magnet or bit of magnetizable material placed at any point in the region of the moving charge will experience a magnetic attraction or repulsion. The electric and magnetic field that results is called an electromagnetic field.
When a disturbance is produced at any point in space by the creation of an electromagnetic field, the disturbance travels through space as an electromagnetic wave. In free space—that is, space devoid of matter or charge—the velocity of all such waves is very close to 3 x cm (1.2 X
inches) per second, which is in fact the velocity of light in free space.
The Electromagnetic Spectrum. Electromagnetic radiation, then, is most simply characterized by its frequency or its wavelength. There is a broad range, or spectrum, of frequencies. One small segment of the spectrum that is extremely important to man is that of visible light. This segment can be seen when sunlight is passed through a prism, forming a band of colors that extends from red at one end to violet at the other. The frequency associated with the red end of the spectrum is about 4 x Hz, and that associated with the violet end is about 8 x
Hz.
However, it is more commonly the practice to refer to the spectrum range in terms of wavelength, and in this respect the unit of length most commonly employed for light waves is the angstrom unit (A). One A is cm, and in this notation the visible light spectrum extends from about 3,800 A at the violet end to about 7,500 A at the red end.
The visible spectrum is only a small part of the whole electromagnetic spectrum, which in terms of wavelength extends very far on either side of the visible region of the spectrum. Beyond the red end come the infrared, or heat, waves, and the radio, or hertzian, waves, which are stili longer. The longest radio waves extend to thousands of meters. On the other side of the visible spectrum, beyond the violet end, come ultraviolet radiation and then roentgen rays, or X rays. Beyond X rays lie gamma rays, with wavelengths of 0.01 A or smaller. These are the shortest electromagnetic waves known.
Source : wikipedia.org
SOURCES OF RADIATION
Consider the example of a metal rod heated in a colorless Bunsen burner flame. It would first be noticed that a hand placed in the vicinity of the rod without touching it would experience warmth. The rod is then said to be emitting heat, or infrared radiation. This can be confirmed by measuring the emitted wavelengths with a suitable instrument. As the rod continues to be heated, it begins to glow a dull and then brighter red, changing to orange and then yellow on further heating, until at last the rod is white hot.
Acceleration of Chorged Particles.
In what sense may the thermal radiation in the above example be considered electromagnetic, as is the visible light? The answer to this question involves the assumption that all materials are made up of atoms, which in turn are composed of positively and negatively charged particles. The electrically negative particles may be more or less tightly bound to the positively charged particles, as in neutral atoms; they may be rather loosely bound; or they may be comparatively free to move from atom to atom, as in the case of metals that are good conductors of heat and electricity.
One of the conclusions of the classical theory of electromagnetism is that whenever a charged partide such as an electron is accelerated, electromagnetic radiation is emitted. In particular, when a charged partide has an oscillatory motion of a definite frequency, electromagnetic radiation of that same frequency will be produced.
The iutensity of the radiation depends on the energy of the oscillation. Thus in the above example, when the metal rod is heated, energy is gradually contributed to its electrons. As they continue to be accelerated they vibrate at higher and higher frequencies, leading to the emission first of heat radiation and then of light radiation.
Electromagnetic radiation at frequencies much lower than those of light or infrared radiation can be produced by the spark discharge between two metal terminals separated in air or in a vacuum and charged to a high difference of electrical potential. Moreover, any metallic conductor in whieh an oscillating electric current is maintained will act as a source of radiations whose frequencies are equal to those of the current. Many kinds of oscillating electrical circuits have been devised that act as sources of radio waves when coupled to appropriate antenna systems. The intensity of the electromagnetic wave emitted by such an antenna—at distances from the antenna that are large compared to the wavelength—varies inversely with the square of the distance of the wave front from the antenna, and it varies directly with the square of the amplitude of the alternating current.
Change in Energy States.
The account thus far has been an oversimplified version of a complex process. A more exact description of electromagnetic radiation demands the quantum theory, which is discussed in more detail below under Radiation and Çuantum Theory. At this point it can be said that the ultimate source of electromagnetic radiation is the atoms of the radiating system. According to the quantum theory of atomic structure, every atom is composed of a positively charged nucleus containing the larger part of the atom’s mass, surrounded by a group of negatively charged electrons that exist in various energy states. When the electrons are “excited” by appropriate means they move to higher energy states, and in returning to their original state they emit radiations whose frequencies equal the decrease in energy involved in the transitions, divided by a constant called Planck’s constant (discussed below in the section dealing with electromagnetic radiation with respect to the quantum theory).
Atoms may be excited by thermal means, as in the heating of the metal rod. They may also be excited by the discharge of electricity at high potential through gases at low pressure, and by the absorption of energy of charged particles from an external source. In a source of radiation in the Xray region of the electromagnetic spectrum, very highspeed electrons impinge on a material target in an evacuated tube and excite the atoms of the target to very highenergy states. Gamma rays are emitted by the nuclei of atoms by means of a rearrangenıent of nuclear structures involving stili higher energy changes, and they are also produced when primary cosmic rays pass through the earth’s atmosphere and strike the atoms and molecules of the air.
PROPERTIES OF ELECTROMAGNETIC WAVES
An electromagnetic wave is the propagation of an electromagnetic field through space. In free space the strength of such a field is described in terms of two fundamental vector quantities, E and H, which refer to the intensities of the electric and the magnetic fields, respectively, of the resultant electromagnetic field. The magnitude of these vectors is proportional to the forces exerted at any point on electric charges and magnets placed in the field. There is also a third vector quantity of an electromagnetic wave that lies in the field s direction of propagation.
Field Vector Properties.
In an electromagnetic wave the electric vector E and the magnetic vector H are perpendicular to each other, and both are perpendicular to the direction of propagation of the wave. This leads to the conclusion that electromagnetic waves are transverse, with no component of the propagated disturbance along the direction of propagation. As a result, it could be assumcd that electromagnetic waves can be polarized—that is, confined to one plane by a device that permits only vibrations in a chosen plane to pass. In fact this conclusion agrees with wellknown properties of visible light and radio waves.
The third vector, which lies in the direction of propagation of an electromagnetic wave, lies at right angles to both the E and II vectors. It has a magnitude equal to the product of these two vectors, and when multiplied by a certain factor it is called the Poyrıting vector. It can be shown that its magnitude gives the rate of flow of energy per unit area of wave front in the wave. Therefore, when averaged over a period of time, the vector represents the average power transmission per unit area, or the intensity of the electromagnetic wave.
Maxwell’s Equations.
For all practical purposes, the vectors E and H are defined by certain mathematical equations that they satisfy. The four equations, known as Maxwell’s equations of , the electromagnetic field, were formulated by the Scottish physicist James Clerk Maxwell in the latter half of the 19th century. Simple in form but mathematically sophisticated, the equations are concerned witlı (1) the nature of the force between electric charges, (2) the nature of the force between magnetic materials, (3) the relationship betwen the intensity of a magnetic field and the electric current that produces it, and (4) the relationship between a changing magnetic field and the electric current or electromotive force that it induces.
From his field equations Maxwell was able to deduce a pair of partial differential equations of the second order, representing the propagation of the field vectors E and H through space in the form of waves. In these two equations there is a certain quantity, c, representing the ratio of the electromagnetic unit of current to the electrostatic unit of current. The value of c was very close to 3 x , and in the equations it was necessary for c to have the dimension of velocity. Thus c had the same value as the measured velocity of light in free space— namely, approximately 3 X
cm per second. This fact led Maxwell to suggest that light waves are in fact electromagnetic in nature.
INTERACTIONS OF RADIATION AND MATTER
Thus far it has been assumed here that electromagnetic radiation takes place in free space —that is, in space that docs not contain any matter. However, when electromagnetic effects take place in material media, it is necessary to introduce other vector quantities besides the electric vector and the magnetic vector. These new quantities, the electric displacement vector D and the magnetic induction vector B, represent the effects of interaction of an electromagnetic field with a material medium.
In the simplest case—that is, when the medium is homogeneous and has the same properties throughout—the electric displacement vector and magnetic vector may be defined in terms of E and H as follows: B = H and D =
E, where if is called the magnetic permeability and k is the dielectric constant of the material medium in question. Further mathematical development of the equations worked out by Maxwell shows that in the material medium the velocity of the electromagnetic wave becomes
(2)
This formula has been found to apply fairly well to transmission of electromagnetic radiation through gases. However, it breaks down rather badly in the case of solids. For example, if the solid is a conductor of electricity, such as a metal, it becomes necessary to modify the equations discussed above in order to take account of the fact that with the transmission of an electromagnetic wave through the solid, an actual current will flow. The flow of the current follows Ohm’s law—that is, the current is proportional to the intensity of the electric field, if the intensity is not too great.
Absorption and Dispersion.
Electromagnetic radiation undergoes absorption and dispersion when it passes through a conducting medium. To say that electromagnetic radiation is absorbed is to say that its intensity is reduced as it flows through space. The reduction is in the ratio l/e —e being the base of Naperian logarithms, or 2.7183 . . . —after the radiation has traversed a distance, in centimeters, given by
(3)
Here is the absorption coefficient and
is the electrical conductivity of the medium in electrostatic uuits. For most good metallic conductors, a is of the order of
in electrostatic units, so for visible light of frequency
Hz, the distance
is approximately 2.5 x
cm. For a radio wave of wavelength 1 cm, or frequency of 3 x
Hz, the corresponding distance is 4 x
cm. This indicates that metallic conductors are very effective absorbers of electromagnetic radiation. It does not pay to try to receive radio waves inside a house whose walls contain much metal, unless an outside antenna is employed.
The term “dispersion” concems the dependence of wave velocity in a material medium on the frequency of the wave. For a good metallic conductor, the velocity is approximated by
(4)
Once more using =
electrostatic units, and f = 3 x
Hz for a 1 cm radio wave, it is found that
= 5 x
cm per second—a considerable reduction from tire velocity of electromagnetic waves in free space.
However, although the above discussion holds fairly well for solid metallic conductors, it does not apply to conductors in general. For example, it breaks down in the case of salt water. Seawater is certainly a good conductor of electricity, yet to a considerable depth it is transparent to visible light while opaque to the longer infrared and radio and the shorter ultraviolet waves. its absorption of electromagnetic radiation therefore does not follow a law such as that in Equation (3), nor does its dispersion of radiation agree with that given by Equation (4).
Interaction of Electromagnetic Radiation with Charged Particles.
Indeed, an adequate theory for the absorption and dispersion of electromagnetic radiation in material media can be developed only by taking into account the interaction between the radiation and the charged particles of the atoms that are the fundamental constituents of the media. In general, a theory of the transmission of such radiation that takes the medium as continuous—that is, not possessing a discrete structure—will prove successful only for very long wavelengths or low frequencies. This situation becomes particularly apparent for transmission through optically transparent solid media such as crystals and glasses.
The physical idea underlying the interaction of an electromagnetic wave with a charged partide such as an electron runs about as follows:
The electrons in an undisturbed medium are subject to forces that cause them to vibrate, at various frequencies, about positions of equilibrium. When an electromagnetic wave of definite frequency encounters the medium and impinges on an electron, it exerts a periodic force on the partide, forcing the electron to vibrate with the frequency of the wave rather than its own natural frequency. The wave disturbance also displaces the position of equilibrium of the electron, introducing what is called a dipole moment.
In order to produce such forced vibration, the electromagnetic wave itself must provide energy. This introduces absorption, since the transferred energy generally is not restored to the electromagnetic wave but is ultimately dissipated as heat. The more closely the natural frequency of the electron vibrations matches the frequency of the wave—the more nearly the electron vibration is in resonance with the wave— the greater is the average transfer of energy from the wave and hence the greater the absorption. At the same time, the production of a dipole moment introduces a change in the dielectric constant , modifying the wave’s velocity as a fupction of frequency. This in turn leads to dispersion.
Reflection and Refraction.
Suppose that an electromagnetic wave is traveling through a certain medium. When it encounters a boundary separating that medium from another one with different properties, such as different permeability and dielectric constant, the phenomena of reflection and refraction are observed.
The law of reflection states that if the boundary between the two media is a plane, and if the incident wave front makes an angle i with that boundary, the reflected wave front will make the same angle with the boundary. That is, the angle of incidence i equals the angle of reflection r. On the other hand, the refracted wave front in the second medium makes the angle 8 with the boundary between the media. This is in accordance with Snell’s law of refraction, which states that
where , and
are the wave velocities in the first and second media, respectively. In the first part of the accompanying figure, the lines AB and CD are the incident and reflected wave fronts, respectively, while the line EC is the refracted wave front.
Lines drawn perpendicular to wave fronts are also useful in wave analysis. Such geometrical lines, called rays, are shown in the second part of the figure with respect to a line NN’ drawn perpendicular to the boundary between the two media. The angle i that the incident ray FA makes with this line is geometrically identical with the angle i that the wave front makes with the boundary, as is the angle r that the reflected ray AD makes with NN’ identical with the angle r that the reflected wave front makes with the boundary. The refracted ray AE forms angle with NN’.
The laws of reflection and refraction follow from the fact that certain boundary conditions on E, H, B, and D must be satisfied over the whole surface separating the two media. The laws include the fact that the incident, reflected, and refracted rays all lie in the same plane and, moreover, that there is no change in the frequency of the electromagnetic wave as it crosses the boundary between the two different media.
Reflection of radiation from metallic conducting surfaces leads to much more complicated phenomena, which are not discussed here. However, in the special case ,in which both media are electrically nonconducting, there are several specific relations connecting the amplitudes of the electric vector in the incident, reflected, and transmitted waves with the angles involved. These relations, known as Fresnel’s formulas, are extensively used in optics. They enable the intensities of the reflected and transmitted radiation to be calculated in terms of the intensity of the incident radiation, and they predict what the polarizations of the reflected and transmitted waves will be. For example, the formulas show that, under certain conditions, complete polarization can take place by reflection at the surface of a nonconducting medium. Thus the intensity of the glare produced when light is reflected at a certain angle from a roadway can be reduced by the use of polaroid glasses.
Wave Guides.
Electromagnetic radiation normally spreads out in all directions from its source, but it can be channeled from one place to another by means of conductors of suitable size and shape. Such conductors are called wave guides, and in action they are somewhat reminiscent of a hollow pipe along which sound can be transmitted, as in a speaking tube or an organ pipe. However, the situation is more complicated in the case of electromagnetic waves.
In general, a wave guide acts as a kind of electromagnetic wave filter. In filter terminology, a hollow cylindrical pipe with conducting walls is a “highpass” filter, meaning that no wave is transmitted until a certain frequency is attained. Short wavelengths tend to get through at the expense of long wavelengths. The cutoff frequency depends on the length and radius of the pipe and is usually a small, nonintegral multiple of the radius. Thus for tubes of reasonable size, only radiation of rather short wavelengths will be transmitted.
Wave guides have proved useful in the propagation of what have come to be called microwaves—that is, electromagnetic radiation in the centimeter wavelength range. They have found employment in the equipment associated with radar, the echoranging technique that makes use of electromagnetic radiation.
RADIATION AND OUANTUM THEORY
In discussing sources of electromagnetic radiation, it was indicated that radiation of relatively low frequency and long wavelength can be handled successfully in terms of the classical theory that considers radiation as resulting from the accelerated motion of charged particles. However, for radiation of shorter wavelength, such as visible light, the situation is different: the eleetrons responsible for the radiation are constituent parts of atoms. The classical electromagnetic theory is unable to account for this radiation, and the quantum theory must be employed as well.
The Ouantum.
At the turn of the 20th century the German physicist Max Planck first develofjed the quantum theory in his attempt to explain the frequency distribution of energy in the thermalradiation region of the electromagnetic speetrum. In order to account for the whole energy distribution curve, Planck found it necessary to assume that energy in electromagnetic radiation is not emitted continuously but in diserete entities called quanta. Each quantum, he determined, is dependent on the frequency f of the radiation, and the amount of energy it represents is in fact equal to hf, where h is Planck’s constant—the ratio of the energy of a quantum to its frequency. This universal constant is equal to 6.62 x erg/second.
According to the quantum theory, all radiation energy is ultimately made up of an integral number of quanta. For long wavelength radiation the magnitude of each quantum is relatively small, and radiation made up of such quanta may effectively be considered as continuous so far as ordinary experience is concerned. However, for the much higher frequencies of visible and ultraviolet light, X rays, and so forth, the size of each quantum becomes so great that the diserete charaeter of the radiation—that is, its quantized nature—cannot always be ignored. Thus for the understanding of emission of highfrequency radiation, quantum mechanics must be employed.
Dual Nature of Radiation.
In spite of the fact that electromagnetic radiation is deseribable in completely logical fashion only in terms of quantum mechanics, visible light and other highfrequency radiations stili manifest such continuouswave properties as interference, diffraction, and polarization when they are subjected to appropriate conditions of measurement involving relatively large numbers of quanta.
On the other hand, there are phenomena that are explicable only on the assumption that light interacts with matter in the form of quanta called photons. A conspicuous example is the photoelectric effect. When light of suffiriently high frequency falls on a metal plate, electrons may be emitted. According to classical electromagnetic theory, the maximum kinetic energy of these socalled photoelectrons should increase with the intensity of the incident light. However, experiment shows that the energy in question depends instead on the frequency of the light, as though the light gave up energy to the electrons in the form of photons of energy hf. The difference between hf and the energy needed to enable the electron to penetrate the surface barrier of the metal equals the maximum kinetic energy of the emerging electrons.
This dual nature of electromagnetic radiation, whereby it can appear in the guise of both wave and partide dependiug ou the experimental conditions involved, received a satisfactory theoretical explanation only through the theory of quantum mechanics.
HISTORY OF THE STUDY OF ELECTROMAGNETIC RADIATION
The history of the study of electromagnetic radiation can best be considered from two points of view: it concerns (1) the development of ideas on the nature of radiation and (2) the evolution of the concept of the electromagnetic field.
Wave Theory and Corpuscular Theory.
The early history of the concept of radiation—primarily light and heat radiation—is a rather tangled affair, in which the notion of the transfer of light and heat by means of the motion of atoms competed with the concept of action at a distance. Since the latter notion was repugnant to many early philosophers, the need arose to discover or “invent” a medium through which light and heat could be transmitted by means of a mechanism akin to wave motion.
The wave theory, which had its roots in antiquity, had come to be accepted as the explanation of the propagation of sound. With light, however, the atomic, or corpuscular, theory persisted as the sole explanation even in the face of the successes of the wave theory in the hands of such 17th, 18th, and 19th century figures as Christiaan Huygens, Thomas Young, and Augustin Fresnel. Isaac Newton had championed the corpuscular theory of light in the late 17th century, and this viewpoint played a dominant role in the study of light until the middle of the 19th century. At that time the first terrestrial measurements of the velocity of light showed that its velocity in water is less than in air—a result that contradicted the prediction of the Newtonian form of the corpuscular theory of light. While this measurement was not auite the crucial experiment it was long hailed as being, it enormously strengthened confidence in the validity of the wave theory.
Yet the wave theory had difficulties of its own. The existence of a wave implies the existence of a medium for its propagation. However, unlike sound, which requires a material medium, light can traverse certain material media but does not demand them. The problem then arose: what is the nature of the nonmaterial, lightbearing medium—or as someone put it, what is “the nominative of the verb ‘to undulate’?” From the viewpoint of the classical mathematical physics of fluids, it is sufficient that the medium possesses elasticity. Yet if it is an ideal elastic fluid, it can transmit longitudinal waves only, while it is well known that light waves are transverse. On the other hand, if the medium is an elastic solid, it should propagate both longitudinal and transverse waves.
Much ingenuity was displayed by physicists in trying to get around this fundamental dimculty. But there were other problems also, and taken all in ali, the elasticmedium theory of light radiation was in serious trouble when the electromagnetic theory came along and proved much more successful.
The Concept of the Electromagnetic Field.
The development of the theory of electromagnetism made possible the prediction of electromagnetic waves. A first step in this development came in 1819, when the Danish scientist Hans Christian Oersted made the discovery that a wire carrying an electric current acts like a magnet—or, as it came to be said, it produces a magnetic field. Oersted’s work was followed by the extensive theoretical and experimental researches of the French physicist Andre M. Ampere on the magnetlike interactions of currentcarrying wires.
Finally, the English scientist Michael Faraday showed in 1831 that it is possible to use the relation between electricity and magnetism to induce an electric current. In order to give a theoretical explanation of this electromagnetism, Faraday revived the concept of magnetic fields introduced by the earlier English scientist William Gilbert in the 16th century. Faraday provided a mathematical representation of such a field in terms of lines of force, and he applied essentially the same idea to the representation of a field produced by electrical charges. Thus he developed in a pictorial form the concept of the electromagnetic field, even evolving the idea that disturbances in an electromagnetic field can be propagated through space. These notions were not received with any great favor by theoreticians in Europe, who tended to favor the concept of action at a distance rather than the propagation of effects through space.
Later in the 19th century, James Clerk Maxwell recognized the importance of Faraday’s field concept and translated it into conventional mathematical terminology. He expressed, in the form of partial differential equations, the Faraday law of electromagnetic induction, the AmpereOersted law for the magnetic effect of an electric current, Coulomb’s law for the force of interaction of electric charges, and the similar law for the interaction of magnetic materials—although the latter was expressed in the fomı that magnetic lines of force, unlike electric lines, are closed lines. In formulating these equations Maxwell observed that, when directly descriptive of the basic experiments involved, the equations do not satisfy the equation of continuity for the density of the electric charge, if density is allowed to vary in time as well as space. This meant that the equations, in the form they originally took, would not permit one to describe the simple discharge of a capacitor.
Maxwell rectified this situation by introducing the socalled “displacement current”—that is, a current postulated to exist in free space, as within dıe capacitor, together with the actually observed electric current in the external connections of the capacitor. This concept of the displacement current, and the insertion of the term into Maxwell’s field equations, led to the prediction of the existence of electromagnetic waves with velocity . In fact, the agreement between the number c as the ratio of the electromagnetic unit of current to the electrostatic unit and its value as the observed velocity of light in free space in centimeters per second had been noted by Continental physicists before Maxwell, but he was the first to give it a genuine physical meaning.
Discovery of Other Forms of Radiation.
In 1887 the German scientist Heinrich Hertz succeeded in showing that the spark produced by the discharge of a capacitor such as a Leyden jar sends out waves that can be detected by a suitable electric resonator—in its simplest form, a circle of wire with a small gap in it. With relatively simple equipment, Hertz was able to measure the wavelength of stationary waves thus generated by measuring the distance between successive nodes of such waves—that is, between points of zero disturbance. From this he was able to calculate the velocity of the waves, and he found that their velocity was in fact equal to that of visible light even though the frequency was very much lower and the wavelength much longer. Hertz wps further able to show that these electromagnetic waves, like ordinary light waves, can be reflected, refracted, diffracted, and polarized. Thus Hertz experimentally verified the prediction Maxwell had made of the existence of electromagnetic radiation.
Not long after Hertz’ studies were made, the English scientist Oliver Lodge carried out even more elaborate experiments along the same lines. Such work led to the development of wireless telegraphy, later called radio communication, to which the Italian inventor Guglielmo Marconi made important practical contributions.
For a time it was thought that the cathode rays discovered by the English scientist William Crookes in 1878 might be a form of electromagnetic radiation, but it was soon confirmed that the rays are actually streams of particles charged with negative electricity—that is, electrons. However, in 1895 the German scientist Wilhelm Roentgen showed that when electrons in a vacuum tube impinge on solid surfaces, a new form of electromagnetic radiation is produced. This radiation is of much shorter wavelength than ordinary light and has the power of penetrating certain matter that is opaque to visible light. These roentgen rays, now called X rays, proved useful in medical diagnosis and in industry. Roentgen rays have also been detected in the radiation reaching the earth from outer space.
In 1896 the French scientist Henri Becquerel discovered radioactivity—that is, the radiation given off by certain atoms. It was soon found that in addition to the alpha and beta rays included in such radiation, which are actually atomic particles, radioactive materials also give off a form of electromagnetic radiation like X rays but of stili shorter wavelengths. These are gamma rays, and they completed the electromagnetic spectrum as it is known today.
Radiation and Relativity Theory.
No treatment of electromagnetic radiation is complete without a reference to the medium that transmits the radiation, some of the theoretical problems caused by the nature of this medium having already been indicated.
In the present article, the electromagnetic medium has simply been referred to as “space.” However, when Maxwell first proposed his theory it was felt necessary to invent a medium, since at that time it was strongly believed that wave motion was impossible without a medium that would bear some analogy to the media in which sound and other waves of ordinary experience are observed. This demand led to the invention of the concept of the luminiferous ether, or ether, for short.
The properties of this ether were obviously mysterious and unlike those of any known wavebearing medium in human experience. An important question arose: Is it possible to detect motion with respect to the ether by means of electromagnetic radiation, as one can detect motion with respect to the air by means of the velocity of sound waves? Maxwell suggested an experiment to answer this question, and it was performed by the American scientist Albert A. Michelson—later with the collaboration of E. W. Morley—at various times from 1881 on. It was found that it is impossible to detect motion with respect to the ether by means of light, or, put in another way, the velocity of light in free space is the same for all observers moving with constant velocity relatively to each other. This means that the equations of the electromagnetic field must retain their form, invariant, for all such observers. It was later shown by Hendrik A. Lorentz and Albert Einstein that for this to be true, the space and time transformations from one such observer to another must be different from that suggested by Newton. Here was essentially the origin of the special theory of relativity, first proposed by Einstein in 1905. In its subsequent development, it has proved to be one of the most important results of electromagnetic radiation theory.