Dive into the world of neurons and the nervous system as we explore 10 key characteristics that define these remarkable nerve cells. Discover their structure, function, and role in transmitting information throughout the body.
Neurons or nerve cells are the cells of the nervous system. These serve to transmit and broadcast information. Networks of neurons are those that communicate by means of nerve impulses the information from the brain to the rest of the body or vice versa.
Neurons are not all the same, but they have different forms depending on their location. All emit nerve impulses by changing polarity. In this way they communicate with each other in order to communicate certain information.
Mental activity necessarily implies the communication of neurons with each other. It is estimated that there are around 100,000 million neurons in the nervous system of humans.
Characteristics Of Neurons
1. Functions
The function of neurons is to communicate information from one part of the body to other parts.
They control, in this way, from the movement of an arm, thoughts and even feelings through electrical signals that are called nerve impulses.
2. Parts
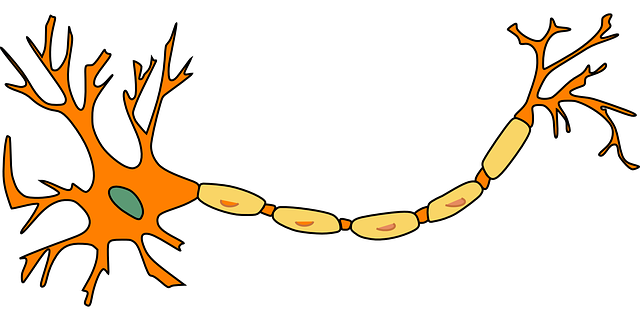
Neurons have different parts that make them up. These parts are:
Dendrites. Dendrites are the branched parts of the neuron that receives the information (nerve impulses) and transport it to the cell body.
Soma, cell body or pericarion. The cell body is the central part of the neuron. In this cell body is the nucleus of the cell.
Axón. The axon is the branch that starts from the cell body and communicates the information to another neuron. These can have different extension depending on the area of the body in which they are.
Myelin Myelin is a white, fatty substance that lines most axons. This has the function of accelerating the nervous impulse. That is, accelerate the information reported up to 90 times per second.
3. Types of neurons
There are different types of neurons:
Sensory neurons These neurons are those that receive stimuli from the environment. For example, the eyes, touch, hearing and transmit signals from different organs to the brain through the spinal cord.
Motor neurons They are neurons that emit signals from the central nervous system to the muscles, thus effecting the movement of these.
Interneurons They must transmit information between sensory and motor neurons.
Relay. They are large neurons that transmit information from one part of the central nervous system to another within it without going through the peripheral nervous system.
4. The synapse
In the final part (called terminal axon) of each cell is a small space called synaptic vesicle (between it and the next neuron). When the information reaches the edge of the axon, some particles called neurotransmitters are released that are released from the axon of the neuron that emits the information.
These neurotransmitters remain in the fluid of the synaptic vesicle. Some of these are lost but many others enter through the synapse to the dendrites of the other cells (neuron that receives the information).
This process occurs between 2 neurons and is repeated infinitely many times since the information leaves a site (brain or sensory organ) until it reaches its destination.
5. Presynaptic and postsynaptic neurons
The presynaptic neuron is called the one that emits the information and is called postsynaptic neuron to the one that receives the information of the presynaptic neuron.
A neuron is presynaptic at a certain moment, but the next moment it becomes a postsynaptic neuron.
6. Types of synapses
There are 3 forms of communication between neurons:
Axodendritic It is the type of connection that makes the branches of the axon (called the terminal button) of the presynaptic neuron with the dendrites of the postsynaptic neuron.
Axosomatics It is connected directly from the terminal button to the soma of the postsynaptic neuron.
Axoaxónicas. The terminal button is connected directly to the axon terminal of the postsynaptic neuron.
7. Stage of neuron formation
In the same way as the human body, the nerve cells are formed from the moment of gestation of the egg zygote with the union of the sperm and the egg.
The process of maturity of the human being is manifested through two instances:
Progressive process This is the first process and occurs through cell proliferation (increased number of neurons), dendritic arborization (when nerve cells increase the number of branching pathways) and myelination.
Regressive process After this process there is a stage called apoptosis or neuronal death where many of the dendrites die after not having synapsed with other neurons.
8. Neurogenesis in pregnancy
This process begins to be generated in the fetus around the 8th month of pregnancy and then allows the formation of the nervous system. This is done through 4 steps or stages:
Proliferation. During this stage, the number of cells increases considerably.
Migration. Migration occurs when the cells leave the ventricular zone of the neural tube to the place where they will definitely lodge. This depends on the site where the neurons are located. This migration is made possible by the glial cells that assist the neurons and function as a sort of path.
Differentiation. The definitive location of the neurons within the nervous system takes place and the interconnections between them are detailed.
Cell death The previous step generates an excessive number of neurons which must inevitably die. There are two modes of cell death: necrosis and apoptosis. The first is unnatural death and the second is the natural death of neurons and only occurs at this stage.
9. Destruction of neurons or necrosis
With the exception of the neuronal pruning stage, different factors can be produced that generate the destruction of the neurons. These can not be recovered. That is to say, after the death of the neurons by cerebral accidents (ingestion of narcotics or excess of alcohol) neurons die and are the only cells that can never be recovered.
10. Adult neurogenesis
Until a few years ago it was believed that after the stage of cell death in childhood development in pregnancy, a stage of cell death preceded, but it was considered that the brain was not able to generate nerve cells again. In other words, if a person had an accident and this affected a certain number of neurons, their recovery was not possible.
This, in a certain way, continues to be maintained although the generation of neural stem cells in adult life is being studied. This does not happen in the whole brain but only in the cells that are in the hippocampus and in the subventricular zone of the lateral ventricles.